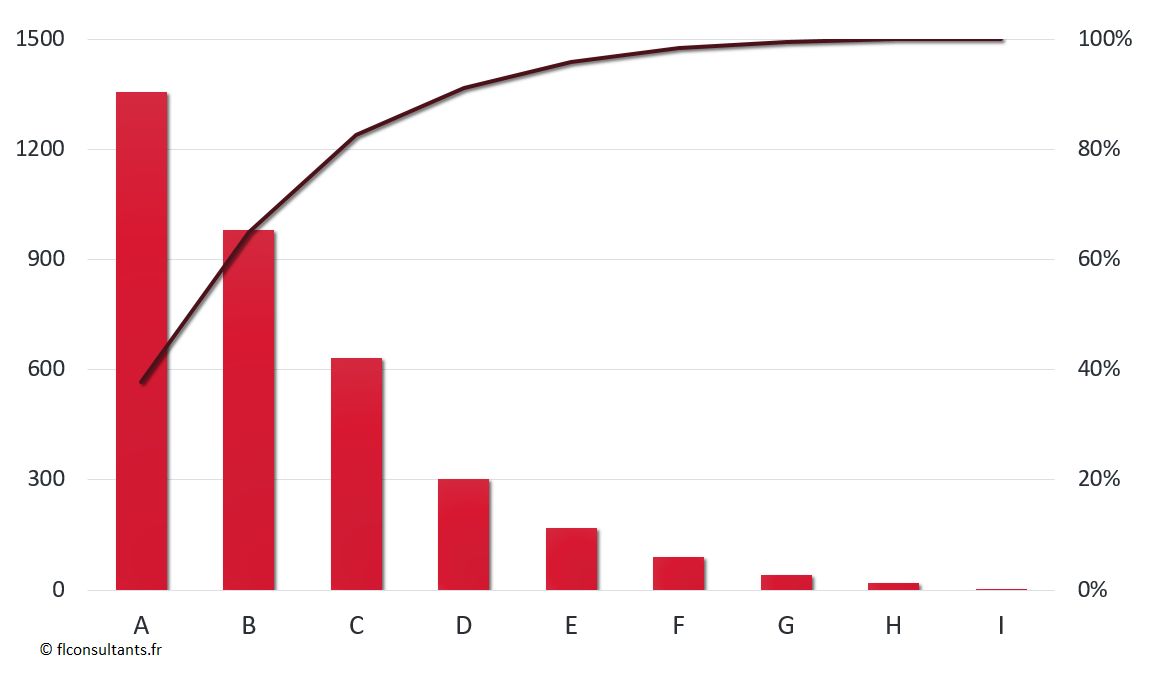
Diagramme de Pareto
Un diagramme de Pareto classe graphiquement les différentes occurrences d’un phénomène, de la plus importante à la moins importante. Par exemple, le classement des différents produits d’une entreprise selon leur chiffre de vente, ou des différentes causes de pannes selon leur fréquence, ou encore le pourcentage de non conformité par familles.
- Récolter les données (CA des différents produits par une extraction de l’ERP, causes de pannes avec leur fréquence par des observations instantanées, etc.)
- Classer les données dans l’ordre décroissant (en les regroupant éventuellement par familles, afin d’avoir un diagramme synthétique)
- Calculer pour chaque classe de données, leur pourcentage par rapport au total (fréquences individuelles), et le pourcentage cumulé (afin d’obtenir une courbe des fréquences cumulées)
| Famille | Valeur | Fréquence | Fréquence cumulée |
|---|---|---|---|
| A | 1356 | 38 % | 38 % |
| B | 981 | 27 % | 65 % |
| C | 632 | 18 % | 83 % |
| D | 302 | 8 % | 91 % |
| E | 170 | 5 % | 96 % |
| F | 91 | 3 % | 98 % |
| G | 42 | 1 % | 99 % |
| H | 18 | 1 % | 100 % |
| I | 1 | 0 % | 100 % |
Principe de Pareto (des 20/80)
Ce diagramme porte le nom de l’économiste Vilfredo Pareto, qui a le premier évoqué le principe des 20-80, principe qui porte son nom. Il avait remarqué qu’une minorité de personnes jouissait d’une majorité de revenu, quel que soit le pays. Plus généralement, on observe souvent qu’un petit nombre de causes expliquent la majeure partie des effets. De manière empirique, on énonce que 80 % des phénomènes sont dus à 20 % des causes.
Dans notre exemple, la courbe des fréquences cumulées atteint les 80% dès la 3ème famille (on est donc plus près des 30-70 dans ce cas). En travaillant sur les familles A, B et C uniquement, on couvre 83 % des cas. Il est a priori inutile de passer trop de temps sur les autres familles. On peut bien sûr choisir le seuil au niveau que l’on souhaite : pour traiter au moins 95 % des cas, on ira jusqu’à la 5ème famille, dans notre exemple.
Ce diagramme sert de base à l’analyse ABC, qui segmente les populations en trois grandes catégories d’importances décroissantes.