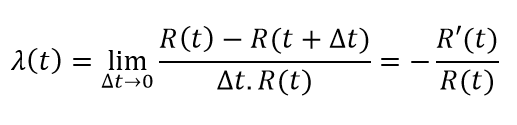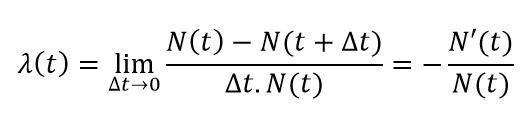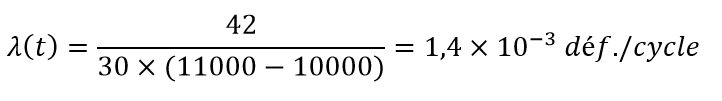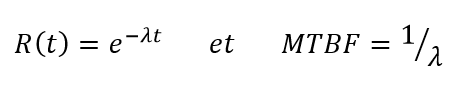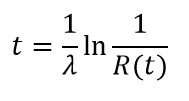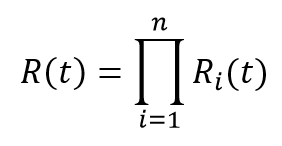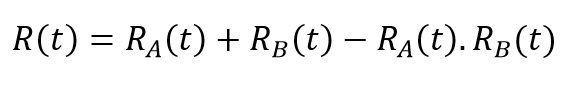Fiabilité et MTBF

Le vocabulaire lié à la maintenance et à la fiabilité, et la définition de leurs indicateurs, n’est pas toujours partagé par tous. La Norme afnor X 60-500 sur la fiabilité, maintenabilité, disponibilité (FMD), tente de standardiser les notions utilisées.

États et temps opérationnels

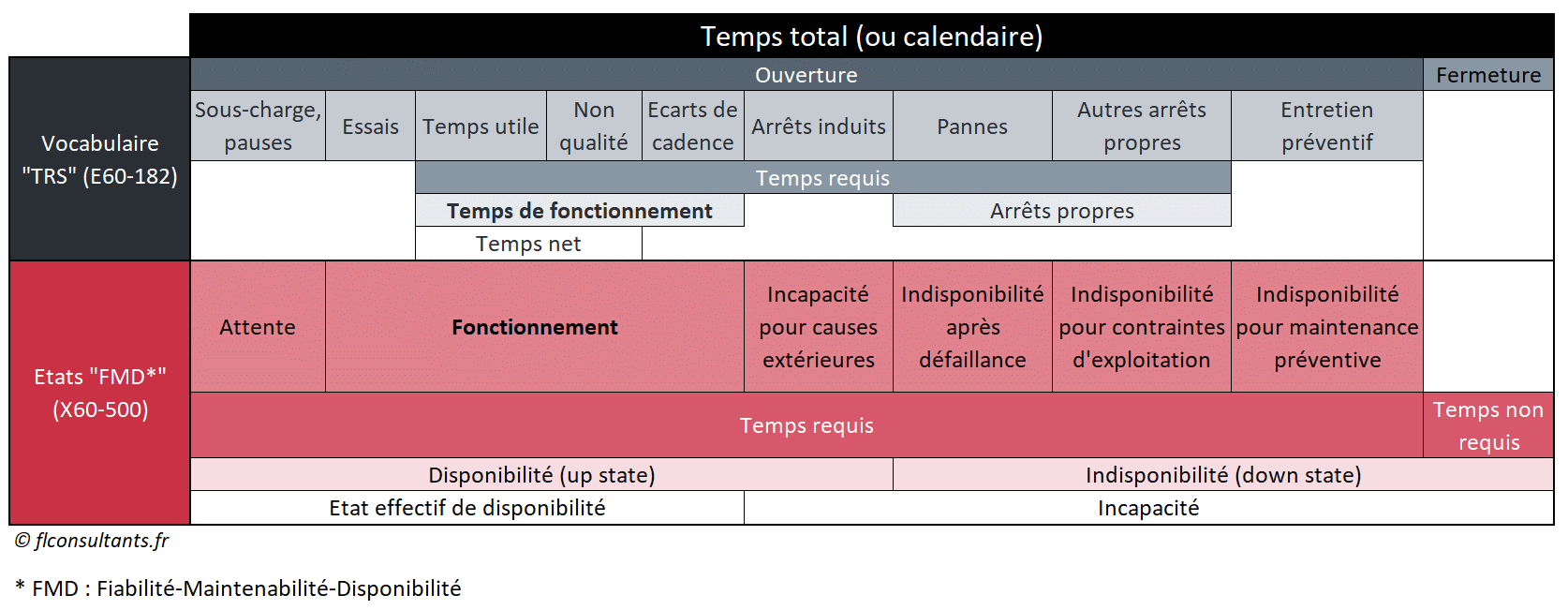
Cette norme définit un certain nombre d’ « états d’une entité » (fonctionnement, attente, …), qui sont parfois différents de ceux (temps utile, temps requis, …) dont parle la norme afnor E60-182 du TRS. D’où les difficultés parfois rencontrées entre les services production et maintenance… Voici une tentative de compilation de ces notions :

Outre des différences de vocabulaire, on note deux écarts notables :

• Le temps requis de la norme FMD comprend, à la différence du TRS, les temps d’arrêts planifiés (maintenance préventive, essais et sous-charge).
• De manière plus marginale, l’état de fonctionnement FMD englobe les temps d’essais (la machine fonctionne pour la maintenance, mais n’est pas requise pour la production). C’est ce temps de fonctionnement qui sert de base de calcul pour les indicateurs de maintenance.

A noter que la norme détaille l’état d’indisponibilité après défaillance en quatre phases :

• Temps de non-détection de la défaillance
• Temps d’appel à la maintenance
• Temps d’indisponibilité pour maintenance corrective proprement dit (lui-même divisé en temps de réparation et en temps annexes : administratifs, logistiques, techniques, de préparation)
• Temps de remise en condition

 

Pannes et défaillances

D’après la norme, une défaillance est

une cessation de l’aptitude d’une entité à accomplir une fonction requise.

Alors qu’une panne est

l’état d’une entité inapte à accomplir une fonction requise, dans des conditions données d’utilisation.

Une défaillance est donc instantanée, et débouche sur un état de panne. L’inaptitude dont il est question doit être intrinsèque à l’entité : les pannes sont des arrêts propres au sens du TRS.

Reste à définir précisément ce qu’est une panne :

• Une défaillance qui arrête totalement l’équipement ? qui l’oblige à fonctionner en dégradé (à vitesse réduite) ?
• Un court-circuit sur une carte peut provoquer une panne. Et un fusible qui lâche ? Le différentiel de l’atelier ? L’alimentation de l’usine (ce serait plutôt un arrêt induit, une cause extérieure) ?
• Relève-t-on une micro-panne de 3 secondes ? De 1 minute ? de 5 minutes ?
• Relève-t-on toutes les défaillances successives d’un même défaut, ou les regroupe-t-on ?
• Un bourrage est-il une panne ?
• …

MTBF – Mean (operating) Time Between Failures

La norme traduit le MTBF par Temps de fonctionnement moyen entre défaillances (FMED). Il s’agit d’un temps de fonctionnement (cf. tableau ci-dessus), et non un temps calendaire ou d’ouverture. Par définition, il exclut également les autres temps d’arrêt. L’appellation courante Temps moyen entre deux pannes est donc abusive : celui-ci serait plutôt le TMED (voir ci-dessous).

Sur une période donnée (qu’on choisira suffisamment longue pour être statistiquement représentative), on peut le calculer comme la somme des temps de fonctionnement divisée par le nombre de défaillances sur cette période.

La norme évoque d’autre part le temps moyen entre défaillances (TMED), comme la moyenne des temps calendaires entre défaillances (que la machine fonctionne ou non), et précise que cet indicateur ne doit pas être confondu avec le MTBF (pendant lequel la machine fonctionne). Cette confusion est pourtant souvent fréquente.

Fiabilité

La fiabilité est donc définie comme

L’aptitude d’une entité à accomplir une fonction requise, dans des conditions données, pendant un intervalle de temps donné.

Le même terme est utilisé pour nommer sa caractéristique :

Probabilité, notée R(t), pour qu’une entité accomplisse une fonction requise, dans des conditions données, pendant un intervalle de temps donné [0;t].

Quand t varie de 0 à l’infini, R(t) varie de 1 (on suppose que l’entité accomplit sa fonction requise à t=0) à 0 (l’entité tombera un jour en panne). La fiabilité, avec la maintenabilité, est une des composantes de la disponibilité.

Taux de défaillance

Le taux de défaillance λ(t) est défini comme :

où R'(t) est la dérivée de R(t). De manière peut-être plus opérationnelle, il est également possible de définir ce taux à partir du nombre d’entités n’ayant pas subi de défaillances à l’instant t N(t) :

Par analogie avec la définition de la vitesse instantanée, on peut comparer le taux de défaillance à la vitesse d’arrivée des pannes.

Exemple

Sur un parc de 30 machines, on observe les défaillances entre le 10 000^e et le 11 000^e cycle. On en relève 42, qui ont été réparées. Le taux de défaillance moyen entre le 10 000^e et le 11 000^e cycle est donc de :

La courbe de λ(t) en fonction du temps a typiquement une forme de baignoire : le taux de défaillance est élevé après le premier démarrage (défauts de jeunesse), ainsi qu’en fin de vie (obsolescence) ; il est plus faible, et relativement constant, entre ces deux phases. Dans ce dernier cas (λ constant), la formule R'(t) = -λ.R(t) permet de poser :

Il s’agit d’un cas typique de fonctionnement en marche courante, notamment pour les composants électroniques (modèle exponentiel de la fiabilité). Applicable à l’exemple précédent, il donnerait un MTBF de 700 cycles environ.

On peut aussi en déduire une durée de vie t associée à un seuil de fiabilité R(t) :

Soit dans notre exemple, une durée de vie pour un seuil de fiabilité de 95% : t = 714 x ln(1,053) = 37 cycles.

Composition des fiabilités

Soit une ligne composée de n modules indépendants en série. La ligne fonctionne si tous ses modules fonctionnent, et il suffit qu’un module soit défaillant pour que la ligne soit elle-même défaillante. La fiabilité globale R de la ligne est égale au produit des fiabilités R_i de chaque module :

Ainsi, pour une ligne de 10 éléments en série, de 99 % de fiabilité chacun, la fiabilité résultante est de 0,99¹⁰ = 90,4 %. Il suffit qu’un seul d’entre eux voit sa fiabilité baisser à 80 % pour que la fiabilité globale chute à 73,1 %.

Dans le cas d’un système redondant constitué de deux éléments en parallèle, la fiabilité globale peut se calculer :

Deux équipements en parallèle, dont la fiabilité individuelle est de 70 %, constituent un système redondant de 91 % de fiabilité globale.