Observations instantanées

Les observations instantanées sont souvent moins coûteuses que des séances d’observations continues, mais leur champ d’analyse est plus spécifiques. Elles peuvent être utilisées pour mesurer :

• Le taux d’utilisation d’un équipement
• Les temps de réalisation d’une opération
• Les coefficients de repos
• Et tout autre taux ou temps d’apparition d’un aléa

Principes statistiques

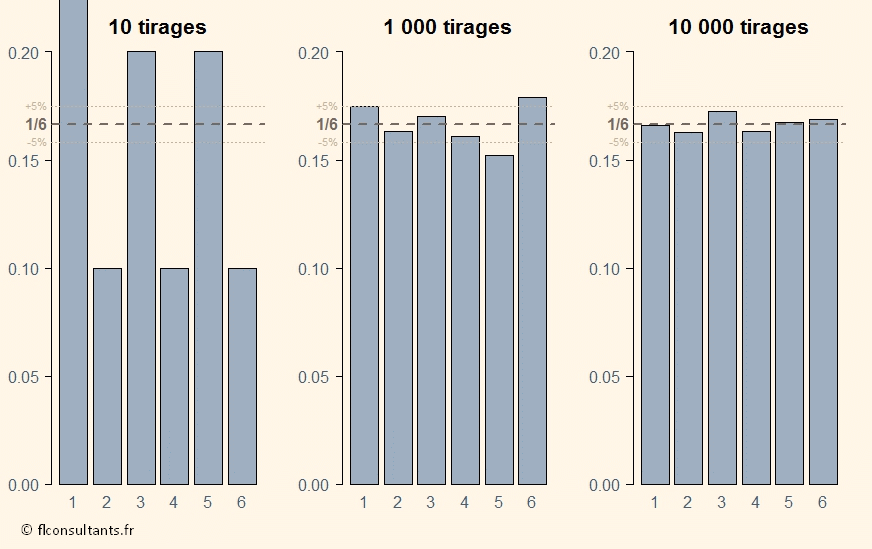
Pour comprendre les fondements théoriques sur lesquels reposent les calculs liés aux observations instantanées, voici un exemple simple. Prenons le cas d’un dé lancé un grand nombre de fois. La probabilité d’apparition de chacun des six chiffres est de 1 sur 6. Pour estimer cette probabilité, il est tout à fait possible de réaliser plusieurs observations de lancers, et noter les résultats. Une dizaine d’observations ne permet pas de retrouver la fréquence de ¹/₆ pour l’un quelconque des résultats (obtenir un 5 par exemple). Un millier en donne une meilleure approximation mais encore en dehors de la précision de ±5% (avec une marge d’erreur de 95%). Dix mille observations permettent de s’approcher plus finement des fréquences réelles.

La méthode des observations instantanées repose sur les mêmes principes. Une machine peut être en production ou à l’arrêt. Si on observe un grand nombre de fois son état instantané, le rapport du nombre de cas où la machine est en marche sur le nombre total d’observations tendra vers son taux réel d’utilisation. Par rapport à l’exemple probabiliste ci-dessus, il faudra en outre s’assurer de réaliser ces observations de manière aléatoire dans le temps, afin d’éliminer tout biais (lié au jour ou à l’horaire, à l’anticipation de l’observation par les personnes impliquées, …).

Dimensionnement des observations instantanées

Le nombre d’observations à réaliser dépend :

• de la précision relative attendue (±5% par exemple, comme ci-dessus) : ε
• de la marge d’erreur acceptable (intervalle de confiance de 95% par exemple)
• de la fréquence estimée (il est plus facile d’observer un évènement fréquent) : f

La formule qui donne le nombre n d’observations instantanées à réaliser est :

\LARGE n=\frac{z_{\alpha/2}^{2}\cdot(1-f)}{f\cdot\epsilon^{2}}

où z_α/2 est le quantième de la loi normale (centrée réduite) donnant l’intervalle de confiance au niveau α. Pour un niveau de confiance à 95%, z_α/2 ≈ 2. Pour un niveau de confiance à 99%, z_α/2 ≈ 3. Travailler avec un niveau de confiance à 95% est le plus fréquent (si on répète l’expérience 100 fois, on n’obtiendra le résultat prédit que dans 95 cas en moyenne). On a donc dans ce cas :

\LARGE n=\frac{4\cdot(1-f)}{f\cdot\epsilon^{2}}

Dans l’exemple du dé à 6 faces, f = ¹/₆. Pour une précision à ±5% (ε = 0,05), la formule donne :

\LARGE n=\frac{4 \times 5/6}{1/6 \times 0,05^{2}}=8000

Prenons maintenant l’exemple d’une machine dont on souhaite connaître le taux de panne. On l’estime à un quart du temps d’ouverture environ. Pour atteindre une précision (relative) de ±5%, n vaudra 4800. Or, cette précision relative de 5% équivaut à une précision absolue d’environ 0,05 × 25 = ±1,25 points de taux de panne, ce qui est sans doute un peu exagéré. Une précision relative de ±10% (soit ±2,5 points de taux de panne) peut être suffisante. n vaut alors 1200, ce qui limite les ressources à allouer pour ces observations.

De manière générale, pour les cas peu fréquents (difficiles à observer), on attend une moins grande précision relative : ε = 20% pour une fréquence estimée de 5% correspond à une erreur absolue de ±1%.

On peut aussi partir d’un nombre d’observations n fixé (pour des raisons de ressources, ou de délai), et en déduire la précision qui peut être obtenue :

\LARGE \epsilon=2\sqrt{\frac{(1-f)}{f\cdot n}}

Ainsi, si n est fixé à 400 et f estimée à 25%, on obtient une précision (relative) ε de ± 17%.

Préparation d’une observation instantanée

1. Bien poser le sujet de l’étude : le phénomène observé (quoi), les acteurs impliqués (qui), le périmètre (où), le nombre d’observation (combien), la manière de réaliser les observations (comment), … : cf. le QQOQCCP.
2. Il faut en particulier bien définir les états qui seront observés : « en panne/en fonctionnement », « en déplacement/immobile ». Il ne doit pas y avoir d’ambiguïté sur ces définitions (surtout s’il y a plusieurs observateurs). Il peut être intéressant d’élargir un peu l’étude (« en panne/en production/en changement d’outil/…), en se basant sur des catégories identiques à celles qu’on pourrait trouver dans le cadre d’une observation continue.
3. Préparer l’outil de relevé des observations (feuille de bâtonnage, smartphone, …). Les horaires d’observations seront prédéfinis, de manière aléatoire, sur l’ensemble des plages où le phénomène est susceptible de se produire. Les horaires ne doivent pas être répétitifs d’un jour sur l’autre (pour limiter tout biais). Il est possible de construire un circuit afin de réaliser plusieurs observations sur le parcours.
4. Réaliser les tournées aux heures prévues, en effectuant une observation ponctuelle à chaque fois.
5. Dépouiller les résultats (calcul des fréquences observées) et vérifier grâce aux formules ci-dessus que la marge d’erreur est toujours acceptable (avec la fréquence f réellement observée).

Ces résultats peuvent servir de base à la réalisation de cartes de contrôle pour un suivi temporel. Les principes statistiques sous-jacents sont identiques : les observations instantanées donnent la moyenne et les limites de contrôle l à ± 3σ (donc pour un niveau de confiance à 99,7%) :

\LARGE l=\pm 3\sqrt{\frac{(1-f)}{f\cdot n}}

Cas d’usage

Occupation machine

C’est le cas classique d’utilisation des observations instantanées. Pour un équipement qu’il n’est pas utile, ou économique, de suivre continuellement en TRS, il est possible d’estimer son taux d’occupation grâce à des observations instantanées. Les différents types d’arrêts peuvent également être calculés (panne, manque opérateur, manque appro, …).

Détermination de temps standards

Sur un total de n observations, n_i concernent une séquence ou une activité. On peut alors calculer un temps observé T_O à partir de la production P (nombre de cycles) réalisée pendant une plage d’ouverture T :

\LARGE T_{O}=\frac{n_{i}}{n}\times\frac{T}{P}

Le temps standard est obtenu en multipliant T_O par l’allure moyenne observée.

Détermination des coefficients de repos

Les coefficients de repos, ou coefficients majorateurs (au sens du BTE), peuvent être estimés par des observations instantanées. Les différents cas d’aléas irréguliers légitimes sont comptés (échanges avec la hiérarchie ou d’autres collègues, pause après un effort, besoins personnels, …). Leur rapport sur le nombre total d’observations donne le pourcentage du coefficient majorateur.

Auto-observations

Il est également possible d’utiliser la méthode des observations instantanées pour effectuer un suivi d’activité. A intervalles aléatoires, je relève objectivement mon activité. La fréquence, et donc le temps, de chacune de mes activités peuvent ainsi être calculés.